Генераторы псевдослучайных чисел: упражнение
В защиту функций с побочным эффектом приводят пример генератора псевдослучайных чисел, возвращающего при каждом вызове случайное число из последовательности, обладающей определенными статистическими свойствами. Последовательность инициализируется вызовом в форме:
random_seed (seed)Здесь seed задается клиентом, что позволяет при необходимости получать одну и ту же последовательность чисел. Каждое очередное число последовательности возвращается при вызове функции:
xx := next_random ()Но и здесь нет причин делать исключение и не ввести дихотомию команда/запрос. Забудем о том, что мы видели выше и начнем все с чистого листа. Как описать генерирование случайных чисел в ОО-контексте?
Как всегда, в объектной технологии зададимся вопросом - зачастую первым и единственным:
Что является абстракцией данных?Соответствующей абстракцией здесь не является "генерирование случайного числа" или "генератор случайных чисел" - обе они функциональны по своей природе, фокусируясь на том, что делает система, а не на том, кто это делает.
Рассуждая дальше, рассмотрим в качестве кандидата понятие "случайное число", но и оно все же не является правильным ответом. Вспомним, что абстракция данных должна сопровождаться командами и запросами, довольно трудно придумать, что можно делать с одним случайным числом.
|
Понятие "случайное число" приводит к тупику. При изучении общих правил выявления классов уже говорилось, что ключевой шаг состоит в отсеве кандидатов. И опять-таки мы видим, что не все многообещающие существительные документа требований ведут к нужным классам. Можно не сомневаться, что данный термин обязательно встретится в любом документе, описывающем рассматриваемую проблему. |
Случайное число не имеет смысла само по себе, оно должно рассматриваться в связи со своими предшественниками в генерируемой последовательности.
Стоп - появился термин последовательность, или, более точно, последовательность псевдослучайных чисел. Это и есть разыскиваемая абстракция! Она вполне законна и напоминает рассмотренный ранее список с курсором, только является бесконечной.
Ее свойства включают:
- команды: make - инициализация некоторым начальным значением seed; forth - передвинуть курсор к следующему элементу последовательности;
- запросы: item - возвращает элемент в позиции курсора.
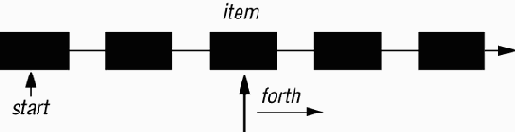
Рис. 5.2. Бесконечный список как машина
Для получения новой последовательности rand клиенты будут использовать create rand.make (seed), для получения следующего значения - rand.forth, для получения текущего значения - xx := rand.item.
Как видите, нет ничего специфического в интерфейсе последовательности случайных чисел за исключением аргумента seed в процедуре создания. Добавив процедуру start, устанавливающую курсор на первом элементе (которую процедура make может вызывать при создании последовательности), мы получаем каркас отложенного класса COUNTABLE_SEQUENCE, описывающего произвольную бесконечную последовательность. На его основе можно построить, например, последовательность простых чисел, определив класс PRIMES - наследника COUNTABLE_SEQUENCE, чьи последовательные элементы являются простыми числами. Другой пример - последовательность чисел Фибоначчи.
| Эти примеры противоречат часто встречающемуся заблуждению, что на компьютерах нельзя представлять бесконечные структуры. АТД дает ключ к их построению - структура полностью определяется аппликативными операциями, число которых конечно (здесь их три - start, forth, item) плюс любые дополнительные компоненты, добавляемые при желании. Конечно, любое выполнение будет всегда создавать только конечное число элементов этой бесконечной структуры. |