О правилах доказательств
Этот параграф предназначен для читателей, склонных к математике, остальные могут сразу перейти к обсуждению в следующем разделе. Хотя основные идеи можно понять и без формального освоения теории языков программирования, полное понимание требует знакомства хотя бы с основами этой теории, изложенными, например, в книге [М 1990], обозначения которой здесь будут использоваться.
Основное математическое свойство последовательного ОО-вычисления было полуформально приведено при обсуждении Проектирования по Контракту:
{INV and pre} body {INV and post}где pre, post и body - это предусловие, постусловие и тело программы, а INV - это инвариант класса. При подходящей аксиоматизации исходных инструкций оно может послужить основой полной формальной аксиоматической семантики ОО-ПО.
Выразим это свойство более строго в виде правила доказательства вызовов. Такое правило послужит фундаментом математического изучения ОО-ПО, поскольку стержнем всякого ОО-вычисления - последовательного, как раньше, или параллельного, рассматриваемого сейчас, - являются операции вида:
t.f (..., a, ...)вызывающие компонент f, возможно, с аргументами такими, как a, для цели t, присоединенной к объекту. Правило доказательства для последовательного случая можно содержательно сформулировать так:
|
Основной последовательный метод доказательства Если можно доказать, что тело f, запущенное в состоянии, удовлетворяющем предусловию f, завершит работу в состоянии, удовлетворяющем постусловию, то для указанного выше вызова можно вывести то же свойство, в котором формальные аргументы заменены фактическими. Каждый неквалифицированный вызов в утверждениях вида some_boolean_property заменяется соответствующим свойством t вида t.some_boolean_property. |
Например, если мы можем доказать, что конкретная реализация put в классе BOUNDED_QUEUE, запускаемая при выполнении условия not full, выдает состояние, удовлетворяющее not empty, то для любой очереди q и любого элемента a приведенное правило позволяет вывести:
{not q.full} q.put (a) {not q.empty}Более формально основное правило доказательства можно выразить, приспособив к ОО-вычислениям известное правило Хоара (Hoare) для доказательства вызовов процедур:
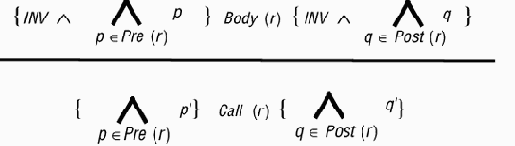
Здесь INV - инвариант класса, Pre (f) - множество предложений предусловия f, а Post (f) - множество предложений постусловия. Напомним, что утверждение является конъюнкцией набора предложений вида:
clause1; ...; clausenЗнаки больших "и" означают конъюнкцию всех предложений. Фактические аргументы f явно не указаны, но выражения со штрихами, такие как t.q' , означают подстановку фактических аргументов вызова вместо формальных аргументов f.
| Из соображений краткости правило приведено в форме, не поддерживающей доказательства вызовов рекурсивных процедур. Однако добавление такой поддержки никак не повлияет на наше обсуждение. Детали, связанные с рекурсией, можно найти в [M 1990]. |
Что изменится в параллельном случае? В предложении предусловия может появиться ожидание только для предусловий в виде t.cond, где t - это сепаратная сущность, являющаяся формальным аргументом подпрограммы, содержащей рассматриваемый вызов. В подпрограмме вида:
f (..., a: T, ...) is require clause1; clause2; ... do ... endлюбое из предложений предусловия, не содержащее сепаратный вызов на сепаратном формальном аргументе, является условием корректности: любой клиент должен обеспечить выполнение этого условия перед каждым вызовом, иначе вызов будет ошибочным. Всякое предложение предусловия, включающее вызов вида a.some_condition, в котором a является сепаратным формальным аргументом, является условием ожидания, которое будет блокировать вызов до своего выполнения.
Эти наблюдения можно выразить в виде правила доказательства, которое заменяет для сепаратного вычисления предыдущее последовательное правило:
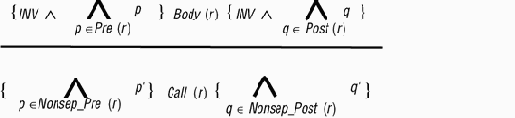
где Nonsep_Pre (f) - множество предложений предусловия f, не содержащих сепаратных вызовов, а Nonsep_Post (f) - аналогичное множество для постусловия.
Это правило частично отражает суть параллельного вычисления. Для доказательства правильности программы все еще требуется доказать те же условия (в числителе), что и в последовательном правиле. Но следствия этого для свойств вызова различны: клиенту нужно обеспечивать меньше свойств перед вызовом, поскольку, как это подробно обсуждено выше, по меньшей мере бесполезно пытаться обеспечить выполнение сепаратной части предусловия; но и на выходе мы получаем меньше гарантированных утверждений. Первое отличие является хорошей новостью для клиента, а последнее - плохой.
Таким образом, сепаратные предложения предусловий и постусловий объединяются с инвариантом как свойства, которые должны быть включены во внутреннее доказательство правильности тела подпрограммы, но они не используются явно как свойства ее вызова.
Это правило также восстанавливает симметрию между предусловиями и постусловиями, дополняя обсуждение, в котором выделялась роль предусловий.